自然も数学も“似のリズム”でできている――自己相似・ドロステ効果・無限鏡との違いを一発解説。
『フラクタル』とは何か――“縮尺を変えても似て見える”世界の設計図(ドロステ効果・無限鏡・自己相似との違いも一発理解)
地図アプリで海岸線をズームすると、ギザギザが消えないのはなぜ?
拡大しても縮小しても、“同じ荒さ”や“同じリズム”が顔を出す――その「続く感じ」に名前があります。

🕒 3秒でわかる結論
フラクタル=縮尺を変えても“部分が全体に似る”構造。
自然(海岸線・樹形・雲・ロマネスコ)から数学図形まで、自己相似が階層的に現れるため、拡大・縮小でも“似”が続いて見えます。
🧒 小学生にもスッキリ
ブロッコリーをちぎると小さいかけらが元の形にそっくりだよね。
大きくしても小さくしても、にている形が出てくる――これがフラクタルだよ。
🥦 ロマネスコってなに?
ロマネスコは、ブロッコリーやカリフラワーの仲間の野菜です。
見た目がとってもふしぎで、トゲトゲした形が何度もくり返されているのが特徴です。
ロマネスコは、
自然がつくった“フラクタルの芸術”みたいな野菜。
食べてもおいしいけれど、見ているだけでも“数学のふしぎ”を感じられる植物です。 🌱
今回の現象とは?
キャッチフレーズQ
- 「海岸線は、ズームしてもギザギザが減らないのはどうして?」
- 「雲や山の**“荒さ”がどの距離でも似て見える**のはなぜ?」
- 「ロマネスコの小さな房が全体そっくりなのはどういう法則?」
このようなことはありませんか?(あるある例)
- 地図アプリで海岸を拡大しても、細かい入江がまた現れる
- 砂浜の波模様を近くで見ても、少し離れて見ても同じリズム
- 樹の枝ぶりが、幹→枝→小枝へと似た分かれ方をくり返す
- 乾いた地面のひび割れが、大・中・小の割れ目で同じ雰囲気
この“スケールを超えるそっくり”には名前と仕組みがあります。
――その正体を、これから一緒にたどっていきましょう。
この記事を読むメリット
- フラクタルの正体が1分でつかめる
- ドロステ効果・無限鏡・自己相似との違いと関係が一発で整理できる
- デザイン・学習・仕事で役立つ**“スケール発想”のコツ**が手に入る
疑問が生まれた物語
夕暮れどき。
私は駅前のベンチに腰を下ろし、今日の散歩の続きを地図アプリでたどっていました。
指先で海岸線を拡大すると、地図の中で小さな入り江が、いくつも、いくつも顔を出します。
さらにズームすると、その入り江の中にも、もっと小さな湾や突端が現れる。
「え……近づいても、形があんまり変わらない?」
思わず眉を寄せて、もう一度指でなぞってみる。
「どこまでズームしても、“ギザギザ”が消えない……なんで?」

海が引くように画面を縮めてみても、大きな地図の輪郭がまた同じように見える。
拡大しても、縮小しても、同じような形が繰り返す――
その瞬間、胸の奥で何かが小さく灯りました。
「もしかして、これは偶然じゃないのかも。
もしかして、“似ている”にも法則があるんじゃないか?」
風が少し冷たくて、スマホを持つ指先がかじかむ。
それでも、私は地図を閉じられませんでした。
だってこの**“似が続く”不思議**が、どうしても気になる。
「どうして世界は、こんなふうに繰り返しを描くんだろう。
自然って、何か同じ設計図で作られているの?」
そう呟いたとき、心の中で“なぜ?”が、静かに、でも確かに芽生えたのです。
――この不思議な“形のリズム”の正体を、次で確かめにいきましょう。
すぐに分かる結論
🧭 お答えします。
フラクタルとは、自己相似(self-similarity/セルフ・シミラリティ)を内蔵した“形のしくみ”です。
縮尺(スケール)を変えても部分が全体に似るため、拡大・縮小をしても**同じらしさ(似のリズム)**が立ち上がります。自然の景観から数理図形、都市や画像生成まで、階層的な繰り返しとして現れます。
噛み砕いていうなら
フラクタル=「似のリズムが、大・中・小で続く」こと。
その“どれくらい複雑か”は フラクタル次元(fractal dimension) という考え方で手ざわりよく捉えられます。
🌉ズームしても薄れない**「似の道筋」**。その正体がフラクタルです。
この“続く似かた”をもっと自分の目と言葉で扱えるように、
次の段落でいっしょに学び、使いこなしていきましょう。
🌿 『フラクタル』とは?
定義(ここだけでOK)
『フラクタル(Fractal)』とは、
**自己相似(セルフ・シミラリティ/Self-similarity)**という性質を
階層的(かいそうてき)に組み込んだ構造のことです。
つまり、
拡大しても縮小しても、部分が全体と似たパターンを示す――
この「似のリズム」が、スケールをまたいで続いて見えるような形。
この考えを数学的に体系化したのが
**フラクタル幾何学(フラクタル・ジオメトリー)**です。
提唱者はフランスの数学者 ベノワ・マンデルブロ(Benoit Mandelbrot)。
1960年代後半にこの言葉を広めました。
自己相似との関係と使い分け
| 用語 | 意味 | 例 |
|---|---|---|
| 自己相似(セルフ・シミラリティ) | スケールを変えても“似る”という性質そのもの | 雲や山の稜線(りょうせん) |
| フラクタル構造 | 自己相似性を仕組みとして内蔵した構造 | ロマネスコやシダの葉 |
| フラクタル図形 | その構造を視覚化した図形 | コッホ曲線・シェルピンスキー三角形 |
| フラクタル幾何学 | フラクタルを数学的に研究する分野 | 複雑な自然形状の解析 |
👉 つまり
自己相似=性質
フラクタル=その性質を持つ構造や図形
という関係です。
フラクタルの2つのタイプ
1️⃣ 完全自己相似(数学的な世界)
拡大・縮小してもまったく同じ形が繰り返すタイプ。
代表例:
- コッホ曲線(Koch Curve)
- シェルピンスキー三角形(Sierpinski Triangle)
- カントール集合(Cantor Set)
2️⃣ 統計的自己相似(自然の世界)
“だいたい似ている”パターンが続くタイプ。
代表例:
- 海岸線
- 雲の輪郭
- 山脈・樹形(じゅけい)・川の分岐
- ロマネスコ(ブロッコリーの仲間)
たとえば海岸線を思い出してください。
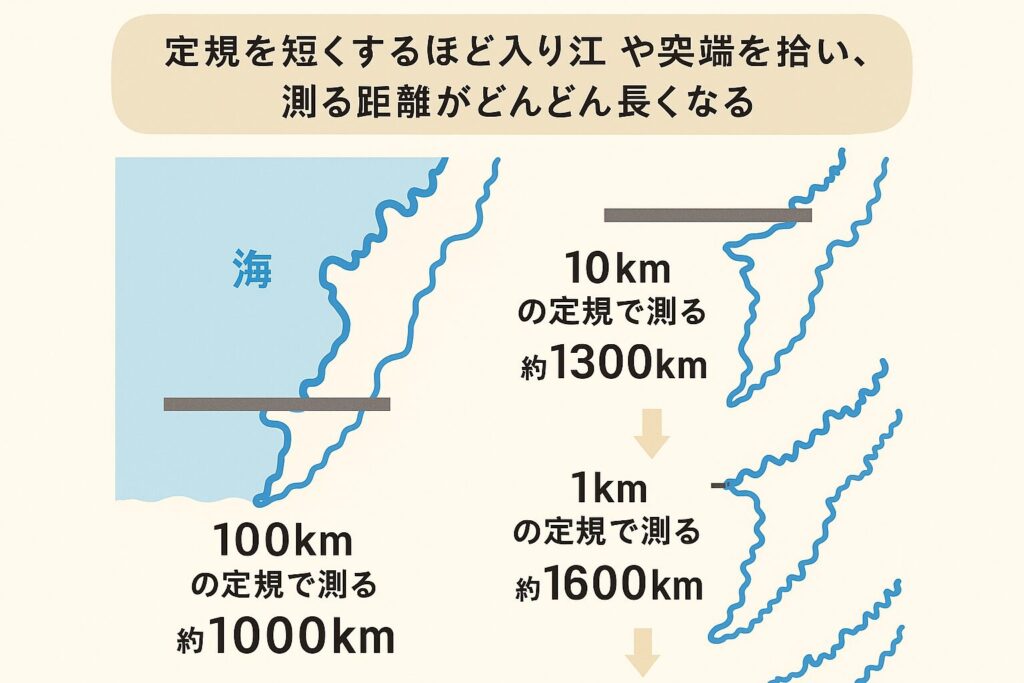
定規を短くするほど入り江や突端を拾い、測る距離がどんどん長くなる――
これが有名な 「海岸線パラドックス」 です。
🌊 海岸線パラドックスとは?
🔹 まず、どんな現象?
地図で海岸線をなぞるとき、
定規(スケール)を短くするほど、測った長さが伸びていく――
これが「海岸線パラドックス(Coastline Paradox)」です。
たとえば
長さ100kmの定規でざっくり測ると「1000km」
長さ10kmの定規で細かく測ると「1300km」
長さ1kmの定規でさらに細かく測ると「1600km」
……と、定規を短くするたびに、海岸線の“長さ”が増えるのです。
「え? 海岸線は1本なのに、定規を変えただけで長さが変わるの?」
と不思議に思いますよね。
それこそが “パラドックス(逆説)” と呼ばれる理由です。
🔹 なぜそんなことが起こるの?
海岸線は、まっすぐな線ではなく、無限に細かい“でこぼこ”の連続だからです。
定規を長くすると、
小さな入り江や突端(とったん)を“見逃して”しまいます。
でも定規を短くしていくと、
今まで見えていなかった細かい凸凹をどんどん拾い始めます。
その結果、測るたびに新しい細部が現れて、距離が伸びていくのです。
🔹 これは「測定できない線」という意味?
正確には「スケールによって長さが変わる線」という意味です。
つまり、“絶対的な長さ”を決められない線なのです。
これを初めて数理的に説明したのが、
フラクタルの父と呼ばれる ベノワ・マンデルブロ(Benoit Mandelbrot) です。
彼は1967年の論文
「How Long Is the Coast of Britain?(イギリスの海岸線はどれくらい長いのか?)」
の中で、この現象を統計的に分析しました。
🔹 フラクタルとの関係
海岸線は、
どのスケールで見ても“だいたい同じ荒さ”が続くという特徴をもっています。
このように「縮尺を変えても似た形が現れる」性質を
数学的に定義したものが、フラクタル(自己相似の構造)です。
つまり、
海岸線パラドックス = “フラクタル的な自然のふるまい”を示す代表例。
海岸線は、完全な自己相似ではなく、
“統計的自己相似(とうけいてきじこそうじ)”と呼ばれるタイプです。
つまり、まったく同じではないけれど、スケールを変えても似た特徴が続くということです。
🔹 もう少し数学的に(やさしく)
マンデルブロは「ボックスカウント法(Box-counting)」という方法で
この現象を定量的に説明しました。
たとえば、
海岸線を一辺がε(イプシロン)の小さな正方形で覆うと、
必要な正方形の数を N(ε) としたとき、
次のような関係が成り立ちます。
N(ε) ≈ ε^(−D)
この D(ディー)が フラクタル次元(Fractal Dimension) です。
この式が意味するのは――
「定規を小さくする(εを小さくする)と、必要なマスの数が爆発的に増える」ということ。
その増え方が、海岸線の複雑さ(フラクタル次元)を表します。
🔹 感覚的にまとめると…
定規を短くすると、より細かい凸凹を拾う
測るほど細部が現れる
結果、長さがどんどん増える
これは「終わりのない複雑さ」=フラクタル構造の一例
だから、
「海岸線は長さを決められない」=“フラクタルな自然”の証拠
なのです。
🔹 たとえ話で言うなら
「毛糸玉をほどいてもほどいても、糸がまだ奥に続いていた」
そんな感覚に少し似ています。
見るたびに新しい細部が顔を出す――
それが、自然が描く“無限の設計図”、フラクタルの魅力です。
フラクタル次元(フラクタル・ディメンション)とは?
フラクタルが「どれくらい細かく、どれくらい複雑か」を表す指標です。
たとえば、
形の上に小さなマス目(サイズをε:イプシロンとします)をかぶせ、
形を覆うのに必要なマスの数を N(ε) とすると、
おおまかに N(ε) ≈ ε^(-D) の関係が成り立ちます。
この D がフラクタル次元です。
つまり、
定規を細かく(εを小さく)するほど、
測る距離や形の細かさがべき乗的(Power law的)に増えるという性質。
難しく聞こえるかもしれませんが、
「拡大しても細部が出てくる=“終わりのない複雑さ”」
と覚えると、感覚的に理解しやすいです。

🌏 なぜ注目されるのか?
私たちが“心地よい”と感じる理由
自然の風景や模様が落ち着く理由――
そのひとつが、フラクタル的な構造にあります。
脳は「多スケールで一貫しているパターン」を見つけると、
情報処理がスムーズになり、**“理解できる安心感”**を得ます。
さらに自然の画像には、
「1/fゆらぎ(いちぶんのえふ・ゆらぎ)」と呼ばれる
粗さと細かさのバランスがとれたリズムが多く含まれています。
たとえば
- 波の音
- 木の葉のそよぎ
- 雲の模様
これらは、規則と変化がちょうどいい比率で混ざっているため、
人間の脳は「安心」と「ほんの少しの刺激」を同時に感じるのです。
それがフラクタルな景色が心地よい理由でもあります。
説明力と実用性
フラクタルは“複雑さ”を少ない数字で表せる力を持ちます。
たとえば
- フラクタル次元で、海岸線の入り組み方を数値化
- **べき乗則(パワー・ロー)**で、都市の広がり方や人口分布を説明
- フラクタル構造で、自然や都市の階層性をモデル化
また、デザインやアート、建築、プログラミングの分野でも活躍します。
“遠くから見ても近くで見ても破綻しない”デザイン――
これもフラクタルの考え方を応用したものです。
「3つ」との違いと関係性
| 名称 | 本質 | 具体例 | フラクタルとの違い |
|---|---|---|---|
| 自己相似(Self-similarity) | スケールを変えても似るという性質 | 雲・山・川 | フラクタルはこの性質を構造として内蔵している |
| 無限鏡(インフィニティ・ミラー) | 光の多重反射による奥行きの連鎖 | 鏡の中に続く光のトンネル | “反射の連鎖”であり、縮尺変化による似ではない |
| ドロステ効果(Droste Effect) | 絵や写真が入れ子状に続く構図 | パッケージの中の自分の絵 | 視覚的演出であり、厳密な自己相似とは限らない |
つまり、
💡 自己相似=性質
フラクタル=その性質をもつ構造や図形
無限鏡=光学的な反射の現象
ドロステ効果=表現・演出の入れ子構図
同じ「似が続く」でも、仕組みと目的がまったく違うのです。
🪞 この章の要点
- フラクタルは「似る」を構造として持つ形
- 自然も数式も、拡大しても縮小しても“らしさ”が続く
- 私たちはその一貫性に安心感と美しさを感じる
よくある質問(FAQ)
Q1. フラクタルと自己相似は同じですか?
A. ちがいます。自己相似は「スケールを変えても似る性質」。フラクタルはその性質が階層的に組み込まれた構造や図形のことです。
Q2. ドロステ効果とフラクタルの違いは?
A. ドロステ効果は「絵や写真の入れ子構図」という表現手法。フラクタルは数理的な構造で、縮尺を変えても似ることが条件です。見た目は似ても、仕組みが別。
Q3. 無限鏡(インフィニティ・ミラー)はフラクタルですか?
A. ちがいます。無限鏡は光の多重反射が奥へ続く物理現象。縮尺を変えて相似が現れるわけではありません。
Q4. 海岸線パラドックスはなぜ起こるの?
A. 短い定規ほど細部の凸凹を拾うため、測るたびに長さが伸びるから。海岸線には統計的自己相似があり、フラクタル次元で複雑さを捉えられます。
Q5. フラクタル次元って、普通の次元(1D/2D/3D)とどう違う?
A. 整数でない次元で複雑さを表す指標。例:滑らかな線は1、面は2だが、海岸線のようにギザギザが続く輪郭は1と2の間になることがあります。
Q6. 「グラフが斜め=パワー則」は本当に正しい?
A. 早合点に注意。両対数グラフで直線に見えても対数正規など他分布で説明できる場合があります。比較・検定で裏取りを。
Q7. ロマネスコは“完全な”フラクタルですか?
A. いいえ。自然物は完全一致ではなく、統計的自己相似が多いです。似ているけれど、少しずつ違います。
Q8. 日常でフラクタルを活かす簡単な方法は?
A. 全体→中→部分の三段観察と、同じ設計原理をスケール連動で使うこと(余白比、影、角Rなど)。「どの定規?」(粒度)を会話・資料で明示するのも効果的。
Q9. デザインが“単調に見える”のはなぜ?
A. 自己相似を入れ過ぎると“テンプレ感”。1か所だけ破調(サイズ比や角度)を入れると、リズムが生まれます。
Q10. 子どもにも説明するコツは?
A. ブロッコリーをちぎる→そっくりを発見。写真を三段ズームで撮って「同じ/違う」を10〜15字で言葉に。見て・撮って・言う、が近道。
Q11. 仕事の資料で“フラクタル発想”を使う例は?
A. 見出し→小見出し→注釈で余白比・文字サイズ比・角R比(例4:2:1)を統一。近景(スマホ)でも遠景(投影)でも破綻しない。
Q12. 学術的にもう一歩深く学ぶには?
A. マンデルブロ(1967)の海岸線論文、高安秀樹の著作などが定番。記事内11章の書籍・体験スポットも参照を。
次の章では、フラクタルの考え方を日常生活やデザインにどう活かせるかを、
具体的な例とともに見ていきましょう。
実生活への応用例
今日から使える
🧪 学習(観察 → 撮影 → ことば化)
三段ズーム:同じ被写体を全体 → 中 → 部分で撮る。
10〜15字メモ:「どこが同じ?どこが違う?」を短文で。
なぞりスケッチ:写真の上から繰り返しの“リズム”を線でトレース。
効果:抽象語(フラクタル/縮尺)に手ざわりが出て、説明が上達。
用語ミニ解説
縮尺(しゅくしゃく/scale):表示の大きさ。
自己相似(じこそうじ/self-similarity):大きさを変えても似ている性質。
具体例
ロマネスコ/シダ/松ぼっくり/雲を3段で撮る → 「尖り」「分岐」「渦」など同じ性質を言語化。
メリット:観察力UP・理科/美術の橋渡し・発表で説得力。
デメリット:完全一致を探すと行き詰まる(自然は“だいたい”が普通)。
💼 仕事・デザイン(多段階の一貫性)
プレゼン資料:見出し→小見出し→注釈で、余白比・角R・アイコン形を“相似的”に統一。
UI(ユーザーインターフェース):カード→セル→チップで影・間隔・角Rを縮尺に合わせて連動。
誌面・ポスター:大見出しの書体と、段落先頭の小見出しに同じ骨格を採用。
用語ミニ解説
相似(そうじ/similarity):形は同じでサイズだけ違う関係。
角R(かどアール):角の丸み半径。スケールに応じて相対値で設計すると統一感。
具体例
ブランド図形(葉・枝・ドット)を大・中・小で繰り返し、“うるさくない”一体感を作る。
コンポーネント設計で“パディング倍率”を統一(例:大:中:小=4:2:1)。
メリット:可読性・再利用性・ブランド一貫性。
デメリット:やり過ぎると単調/テンプレ感 → 意図的な一箇所の破調で回避。

🎥 写真・映像(スケールで物語る)
対置ショット:ドローン遠景の河川分岐 → 直後に地上の枝葉の分岐。
三幕構成:前景→中景→遠景に“同じ形質”を置き、奥行きと統一感を強化。
テクスチャ連鎖:岩肌→石→砂の“ざらつきの連続”で“世界観の一貫性”。
メリット:“わかった感”+“広がり”が同居。
デメリット:似すぎる画の連打で飽和 → 角度・光・比率を変えて微差を作る。
🧭 思考整理(自己相似WBS)
同じ文型で目標→大課題→中課題→小タスクを分解(例:動詞はじめ)。
時間帯のスケール(週→日→1時間)も相似で割り当てると、上から俯瞰/下から積上げがかみ合う。
用語ミニ解説
WBS(ダブリュー・ビー・エス/Work Breakdown Structure):作業分解構造。
メリット:道筋が同形で迷いにくい・引き継ぎしやすい。
デメリット:細分化しすぎで管理コスト増 → “3±1段”を目安に。
🌍 世間での受け入れ・利用のされ方
建築・景観:街路樹や街区に階層性を与え、近距離/遠景どちらでも“秩序”が読める設計。
CG/ゲーム:プロシージャル(手続き型)生成で、自然物(山・雲・海)のらしさを低コスト表現。
データ可視化:多解像度(マルチスケール)の指標・地図で、一目で“構造”を伝える。
注意点・誤解されがちな点
🙅♂️ よくある誤解
「繰り返し模様=フラクタル」
→ いいえ。縮尺を変えても似ることが条件。周期タイルは別物。
「自然は完璧な自己相似」
→ いいえ。多くは統計的自己相似(“だいたい同じ”)。成り立つ範囲が限られる。
「無限鏡/ドロステと同じ」
→ 原理が別:無限鏡=反射の連鎖(物理)/ドロステ=構図の再帰(表現)/フラクタル=形のしくみ(数理・自然)。
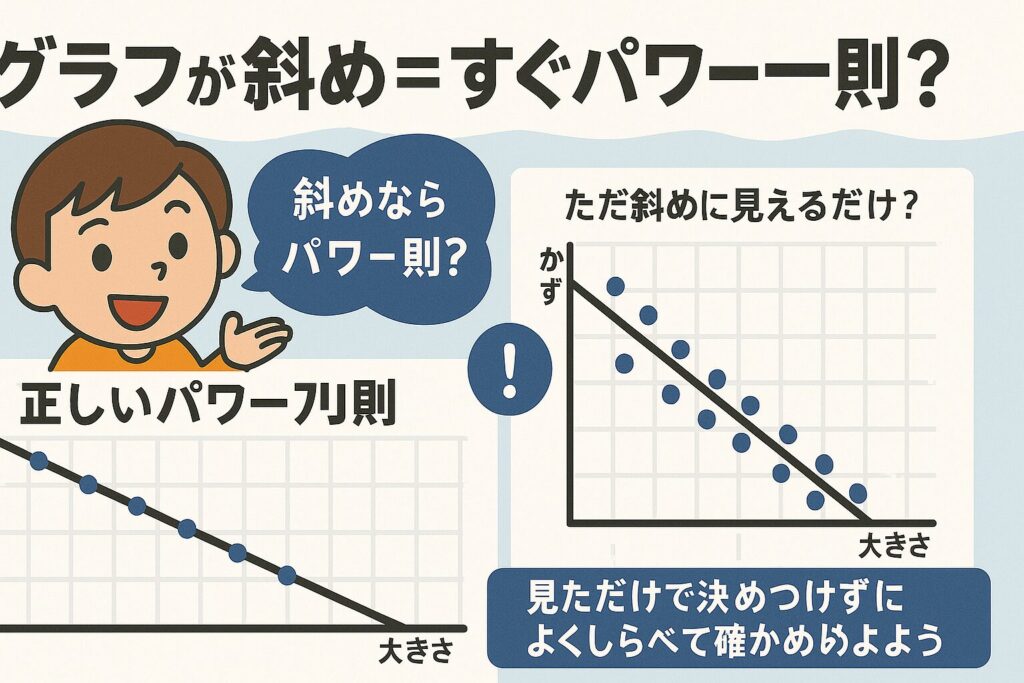
「グラフが斜め=すぐパワー則」
→ 両対数(log–log)の見かけ直線は錯視になりがち。対立仮説(対数正規など)と検定が必要。
用語ミニ解説
統計的自己相似:完全一致ではなく分布や粗さが“だいたい同じ”。
パワー則(パワー・ロウ/power law):数量がべき乗で縮尺に依存する関係。
🍎まず「パワー則(パワーロウ)」ってなに?
「パワー則」は、“大きいものほど少なく、小さいものほどたくさんある”というような関係のことです。
たとえば
山の高さ → 高い山は少ないけど、低い山はたくさんある
都市の人口 → 大都市は少ないけど、小さな町はたくさんある
こういう関係をグラフにすると、「まっすぐな斜めの線」になります。
📈では「グラフが斜め=すぐパワー則」とは?
フラクタルや自然現象を調べるとき、両対数グラフ(りょうたいすうグラフ:Log–Log graph)という特別なグラフを使うことがあります。
これは「数を“そのまま”ではなく、“大きさの比”で見る」グラフです。
このとき、グラフに斜めの直線が現れると、
「これはパワー則だ!」と思い込みやすいんです。
でもそれは間違いのもと。
なぜなら、“なんとなく斜め”に見えるだけでも、
本当のパワー則じゃないことがあるからです。
🧠たとえるなら…
黒板にいくつか点を描いて、なんとなく右下がりに見えるとします。
でもそれを「まっすぐな線」と信じこんで、
「法則を見つけた!」と思ってしまう――
これが「グラフが斜め=すぐパワー則」と言われる“勘違い”なんです。
💬ひとことで言うと
グラフが斜めに見えても、それだけで法則と決めつけないでね。
見た目の“まっすぐ”に、かならず“確かめ”を足そう。
⚠️ 危険な考え方(NG)と理由
なんでもフラクタル化:根拠のスケール範囲を示さない過剰一般化。
完全一致の強要:自然の魅力は“似て非なる”ゆらぎにもある。
装飾のための装飾:自己相似を足しすぎて主役の可読性を損なう。
🤔 なぜ誤解が生まれるのか(認知のクセ)
アポフェニア(パターン過剰検出):意味ある繰り返しを見つけすぎる傾向。
ズーム時代の切り取り:スマホで“似に見える瞬間”だけを偏って保存しがち。
言葉の混同:反復/相似/再帰/スケール不変の違いが曖昧になりやすい。
✅ 誤解を避けるチェックリスト
最低3スケール(全体・中・部分)で確認した?
どこまで成り立つか(スケール範囲)を書いた?
目的(説明/演出/分析)を先に決め、フラクタルは引き立て役にしている?
無限鏡/ドロステと横並びで違いを補足した?
可能ならボックスカウントでフラクタル次元の雰囲気を押さえた?
参考ミニ式(かんたん版)
N(ε) ≈ ε^(-D):小さな正方形(辺 ε)で覆う個数 Nが、縮尺に応じてべき乗で増える。
「細かく見るほど“複雑さがまた現れる”」と覚えればOK。
🧭 行動の一歩
- まずは同じ被写体を三段で撮る。
- 似と違いを10〜15字で書く。
- 仕事では倍率ルールを1つ決める(例:余白・角Rを4:2:1)。
- 可視化・議論では**「どの定規?」(粒度・縮尺)を必ず明示**。
合言葉:「似の道筋」を道具に。
使うほど、世界は同じで少し違うその美しさを見せてくれます。
おまけコラム
海岸線は“どの定規”で変わる?
結論だけ先に
同じ海岸線でも、どの定規(ものさし)で測るかで“長さ”は変わります。
短い定規ほど細部のデコボコを拾う → 長さが増える。
これが有名な海岸線パラドックスです(パラドックス=一見矛盾に見える現象)。
なぜそう見える?(フラクタル次元の直感)
海岸線の“ギザギザ”は、ズームしても似た粗さが顔を出す傾向があります。
この「スケールを変えても複雑さが再出現」する感じを、数学では
フラクタル次元(fractal dimension/ディメンション)で捉えます。
厳密な式は不要ですが、雰囲気だけ👇
箱カウント法(Box-counting/ボックス・カウント)
写真に小さな正方形の格子を重ねる → 形を覆うマスの数を数える。
格子の一辺(ε:イプシロン)を小さくしていくと、必要なマス数 N(ε) が増える。
多くの自然の輪郭では、ざっくり
N(ε) ≈ ε^(-D)(ディー=フラクタル次元)
のように変わることが観察できます。
要するに「定規が細かいほど、また細かい凹凸が出てくる」。
“定規を持ち替える”と世界が変わる
3つの日常例
地図アプリ:ズームインすると岬・湾の細部が出現 → 距離が“伸びる”。
ビジネスKPI:日次と5分粒度では“変動の荒さ”が別物に見える。
写真の解像度:ピクセル(画素)を細かくすると、境界が長く見える。
30秒ナプキン実験(テーブルでOK)
海岸線や雲の写真を用意
上に格子(方眼紙でもスマホの透明グリッドでも)を重ねる
格子サイズを1/2にして、覆うマス数の増え方を比べる
→ 「細かい定規ほど、複雑さがまた顔を出す」が体感できます。
教訓(測り方を明示する)
距離・変動・頻度の議論では、“どの定規(縮尺・粒度)か”を必ず書く。
見解のズレの大半は、定規の違いから生まれます。
フラクタルの視点は、「尺度を変えると結果も変わる」を先に自覚するための“合言葉”です。
まとめ・考察
3行で総括
フラクタル=自己相似(セルフ・シミラリティ)が階層的に組み込まれた構造/図形。
自然では統計的自己相似として現れ、フラクタル次元で複雑さの度合いを指標化できる。
無限鏡=反射(物理)/ドロステ=入れ子(表現)/自己相似=性質(数理・自然)で整理すると混同しない。
なぜ私たちは惹かれる?(認知の視点)
脳は多スケールの一貫性を見つけると処理がラク(=心地よい)。
しかも、“少しずつ違う”統計的自己相似が飽きにくさを生む。
つまり、安心(予測)と驚き(微差)のバランスが快に繋がる。
今日から使える“フラクタルの目”
学び:同一被写体を全体→中→部分で撮る → 「同じ/違う」を15字でメモ。
デザイン/UI:大・中・小で余白比/角R/影を相似に → 近景・遠景どちらでも破綻しない。
分析:グラフやKPIは粒度(定規)を明示 → 思い込みを減らす。
思考:章→節→項を同じ“文型ルール”で統一 → 論理の自己相似で伝わりやすく。
落とし穴(よくあるNG)
なんでも「フラクタルだ!」と言い切る(※範囲を書かない)。
自然に完全一致を求める(※多くはだいたい同じ=統計的)。
無限鏡/ドロステと混同(※原理が別)。
→ 回避のコツ:最低3スケールで確認+成り立つ範囲の明記+目的(説明/演出/分析)を先に決める。
考察(2粒のメタ認知)
高尚:フラクタルは複雑の中の秩序をすくい上げる審美の道具。
ユニーク:思考や文章も自己相似にできる。上から下まで同じリズムで書くと、読まれる。
小さな宿題(週末15分)
被写体を1つ(ロマネスコ/シダ/雲/樹形)選ぶ
全体→中→部分の3枚を撮る
各写真に「同じ/違う」を15字でメモ
余力があれば、格子を重ねて箱数の違いを比べる
→ 次に世界を見ると、スケールで景色がつながる感覚が手に入ります。
ひとこと余韻
拡大の先にも、縮小の先にも、似の道筋は続いています。
“定規を持ち替える”たびに、世界は同じ顔で、少し違う表情を見せてくれるはずです。
🌱 ――ここから先は、あなた自身の“定規”を持つ番です。
今回の現象で出てきた語彙(ごい)や考え方を増やして、
日常の中に潜む“フラクタル的な世界”を、自分の言葉で語れるようになっていきましょう。
見慣れた風景も、思考のパターンも、
「スケールを変えると同じような形が現れる」という視点で見ると、
きっと今までとは違う奥行きのある景色が見えてきます。
応用編
日常を“フラクタルの目”で見る
🔍 見る角度を変えると、いつもの景色が変わる
フラクタルは「自然界の幾何学(きかがく)」にとどまりません。
私たちの日常の思考や行動、言葉の使い方にも“自己相似(じこそうじ)”的な構造が隠れています。
たとえば――
会話:全体の話題 → 中心の話 → 具体的な例。
この流れも“部分が全体を映す”フラクタル構造です。
学習ノート:章 → 節 → 項を似たリズムで書くと、理解の層がつながります。
散歩道:地図で見ると枝分かれした川や道路が、
近くで見ると木の枝や葉脈とそっくり。
「似ているけれど違う」
――その微妙な差にこそ、世界の豊かさがあります。
💡 フラクタル発想を“実践”に活かす
学びに使う
一つのテーマを「全体 → 中 → 部分」の三段階で観察・撮影。
「どこが同じ?どこが違う?」を短文で言語化。
→ 理解が立体的になり、説明力が上がります。
仕事やデザインに使う
資料構成やデザインを自己相似的に統一。
例:見出し→小見出し→注釈まで“余白比”や“角丸”をスケール連動。
→ 一貫性が生まれ、伝わりやすくなります。
心の整理に使う
モヤモヤした考えを「大きなテーマ → 小さな行動」に分け、
同じ言葉のリズムで書き出す。
→ 頭の中の“形”が見えて、行動の優先度も整います。
🌊 まとめると
フラクタルの考え方は、複雑を“見える形”にする道具。
数学でも芸術でも、
“似のリズム”を意識することで、
理解・デザイン・思考がスケールを超えてつながるようになります。
🌉 拡大しても縮小しても、
私たちの中にあるリズムや構造はどこか似ている。
そのことに気づいた瞬間、世界はもう少しだけやさしく、深く見えてくる。
――ここから先は、あなたの観察の旅。
“似の道筋”をたどる目を、自分の世界で育てていきましょう。
更に学びたい人へ
📚 書籍紹介
『フラクタル : 混沌と秩序のあいだに生まれる美しい図形』
著者:オリヴァー・リントン/翻訳:駒田 曜
特徴:豊富なビジュアルとともに、フラクタル図形(例:コッホ曲線、マンデルブロ集合など)を視覚的に楽しみながら理解できる入門書。
おすすめ理由:図や写真が多く、小学生~初学者にもとっつきやすい。フラクタルの「拡大しても似て見える」直感をつかむのに最適。
『フラクタルって何だろう : 新しい科学が自然を見る目を変えた』
著者:高安 秀樹・高安 美佐子
特徴:自然界のフラクタル(山並み・雲・海岸線・株価のゆらぎなど)を多数の事例で紹介し、読み物としても楽しめる構成。
おすすめ理由:数理背景に少し踏み込みたい中級者向け。自己相似・フラクタル構造を「なぜ?」という視点で掘り下げたい人にぴったり。
『フラクタル科学(新装版)』
著者/編集:高安 秀樹
特徴:自然科学・複雑系・統計的自己相似・スケール不変性など、フラクタル現象を理論的・応用的に広く扱う。
おすすめ理由:数式・研究背景・応用事例に関心がある人、デザイン・分析・研究にも使いたい人に向いている。
🗺 体験できる場所
中谷宇吉郎 雪の科学館(石川県加賀市)
特徴:雪の結晶という“自己相似的な自然現象”をテーマにした科学館。展示・観察・実験を通じて「縮尺が変わっても似る」世界を実感できる。
おすすめ理由:理論だけでなく、実物・見えるもの・手を動かす体験を通じて学びたい人に適している。
名古屋市科学館(愛知県名古屋市)
特徴:光・鏡・視覚・科学体験など、スケール感・反射・構図といった“見え方の法則”を体験できる展示が充実。
おすすめ理由:家族連れ・初めて科学館に行く人にも入りやすく、「自分の観察眼を育てたい」という人に向いている。
日本科学未来館(東京都お台場)
特徴:自然・計算・生成の交差点として、マルチスケール・複雑系・形の生成など展示。フラクタル的な概念を“未来の技術・デザイン”という視点で捉えられる。
おすすめ理由:自己相似・フラクタル構造の“数理/生成”側に興味がある人、将来的に創作・研究にも使える知見を得たい人に特に有効。
✅ 読書+体験の両輪で“フラクタル”という視点を言葉と感覚の両面から深めましょう。
ぜひこれらを活用して、世界を“拡大・縮小”して見る目を育ててください。
✨ 疑問が解決した物語
朝の光が、カーテンのすき間からやわらかく差し込んでいました。
机の上には昨夜まで開いていたノート。
そこには、何度も書きかけては止まった「似ているとは?」の文字が並んでいます。
私はスマホの地図をもう一度開き、あの海岸線を見つめました。
前に感じた“終わらないギザギザ”が、今日は少し違って見えます。
「そうか……“同じに見える”のは偶然じゃないんだ。
自然そのものが、縮尺を変えても似ている“フラクタル”の仕組みでできているんだ。」
拡大しても、縮小しても、
“部分が全体に似る”――それは世界がもつリズム。
違うのではなく、“続いている”のだと、ようやく腑に落ちました。
地図を閉じて、外に出る。
街路樹の枝ぶり、川の流れ、ビルの影の形。
どれも少しずつ違って、でもどこか同じ。
「私たちの思考も、毎日の出来事も、
大きく見れば似たリズムの中でくり返しているのかもしれない。」
そう思うと、不思議と心が落ち着きました。
“完全な同じ”を探すより、
“似が続く”中にある秩序を感じ取るほうが、
世界はずっと面白く見える。
私はノートを開き、最後の行に書き加えます。
「フラクタル――世界が似を重ねてつくる設計図」

ページを閉じながら、ふと思いました。
もし世界が“似のリズム”でできているなら、
あなたの中にも、そのリズムが流れているのかもしれません。
――次に何かを観察するとき、
“どこまで似ている?”と、自分の目でたしかめてみませんか。
🌙 文章の締めとして
静かに夜が降りてきます。
街の灯りが、水面のようにゆらいで見えました。
私は今日、地図の中だけでなく、
世界の“似かた”を少し理解した気がします。
それは公式や数式ではなく、
ただ「そう見える」という、確かな感覚。
フラクタルという言葉を知っても、
世界が急に変わるわけではありません。
でも、同じ風景が少しだけ違って見える。
それだけで、なんだか得をした気がしました。
雲の流れの中に、山の稜線の中に、
そして人の心の動きの中にも、
“似のリズム”は息づいているのかもしれません。
もし明日、また何かを観察するとき、
少しだけ立ち止まって、
「これもフラクタルかも」と感じてみてください。
それはきっと、
あなた自身の中にある“世界の設計図”を
そっと覗く一瞬になるでしょう。
注意補足
本記事は、信頼できる基礎知識と公開情報をもとに、
著者が個人で検証できる範囲を中心にまとめています。
自然現象には例外や幅があり、ここでの説明が唯一の正解ではありません。
研究の進展や測定スケールの違いにより、解釈は更新される可能性があります。
この記事が、自分の“定規”を持って世界を見る入り口になれば幸いです。
もしこの小さな“フラクタル”の入口が、
あなたの中に新しい“似の連なり”を生んだなら、
次はぜひ、本や資料の中で――
より深い層のフラクタルを、あなた自身の言葉で探してみてください。

最後まで読んでいただき、
本当にありがとうございました。
世界の“似”を見つめるこの旅も、
また次の“フラクタル”へと、静かに続いていきます。 🌿







コメント