身のまわりのロマネスコや雲の形にひそむ“似て続く”法則。
科学とアートをつなぐ、形のリズムの読み解き方。
🔍 拡大しても同じに見えるのはなぜ?――自然がくり返す『自己相似(セルフ・シミラリティ)』という不思議な法則
朝、キッチンでロマネスコ(カリフラワーの仲間)を切ったとき、
ふと気づきませんか?――小さなツブが、大きな形とそっくり。
拡大しても、縮小しても、まるで**“自分のコピー”が重なっているよう**に見える。
それが「自己相似(セルフ・シミラリティ)」という、自然界に潜む不思議な秩序の正体です。

🕒3秒でわかる結論
『自己相似(セルフ・シミラリティ)』とは、
大きさを変えても形のパターンが似ている性質のこと。
自然界ではブロッコリーやシダの葉、雪の結晶などに見られる現象で、
**部分が全体に似る“フラクタル構造”**とも呼ばれます。
🧒小学生にもスッキリわかる説明
たとえばブロッコリーを小さくちぎると、
小さなかけらがもとのブロッコリーにそっくりですよね。
これが『自己相似』です。
小さい中にも同じ形がある。それが自然が作る“ふしぎなルール”なんです。
🌱今回の現象とは?
🪞拡大しても同じに見えるのはなぜ?――それが“自己相似”の法則
こんなこと、感じたことありませんか?
- 📷 スマホで雪の結晶を拡大したら、小さな枝も“同じ形”で伸びていた
- 🌿 シダの葉を近くで見ると、小さい葉が大きな葉と同じ形をしていた
- 🌊 海岸線の写真をズームしても、ギザギザのリズムが変わらない
- 🌇 ドローンで見た街の道路が、木の枝みたいに枝分かれして見えた
「どうして大きくしても小さくしても、同じような形になるんだろう?」
実はこの“スケールを超えるそっくり”には、ちゃんとした名前があります。
それが——『自己相似(Self-Similarity)』という現象です。
「同じようで違う、違うようで同じ。」
そんな自然のパターンの不思議を、これから一緒に解き明かしていきましょう。
💡この記事を読むメリット
- 自己相似のしくみが1分で理解できる!
- 無限鏡・ドロステ効果との違いが一目でわかる!
- デザインや思考整理に使える**“スケールを意識する発想術”**が学べる!
✨疑問が浮かんだ物語
夕方、買い物帰り。
小学6年生の美咲は、台所で※ロマネスコを切り分けていました。
切り口のツブを見て、ふと手を止めます。
※カリフラワーとブロッコリーの仲間で、サンゴのような螺旋状の形が特徴の野菜です
「…あれ?小さいのに、大きいのと同じ形してる…?」
ツブをひとつ、さらにちぎって並べてみる。
どれも似た形で、くるくると同じ模様を描いています。

「どうしてだろう? 切っても切っても、同じ形が出てくるなんて」
その瞬間、胸の奥で**“なんで?”**という小さなランプが点きました。
不思議、謎、でもどこか美しい。
「この形には、何かの法則があるのかもしれない——」
そう感じた美咲は、じっとそのツブを見つめました。
次へ、その“形の秘密”を探しに行きましょう。
🔍すぐに分かる結論
🧭 お答えします。
「自己相似(Self-Similarity/セルフ・シミラリティ)」とは、
拡大・縮小しても形のパターンが似ているという性質のことです。
自然の中では、ブロッコリー、雪の結晶、シダ、山脈、雲、川の流れなど、
さまざまな場所にこの法則が現れます。
たとえばロマネスコのツブは、
ひとつのツブが“全体の形”と同じ構造をしているため、
どこまで拡大しても似た模様が見えるのです。
🧩噛み砕いていうなら
自己相似とは、形の中に形が、似たように繰り返されていること。
いわば“形のリズム”がスケールを超えて続いている状態です。
似ているようで、少しずつ変わる——そのバランスが自然の美しさを生んでいます。
🌈この“終わらないそっくり”の正体を、
もう少し深くのぞいてみましょう。
次の段落では、自己相似の科学とデザインの法則を、
あなたの目で確かめていきましょう。
『自己相似(セルフ・シミラリティ)』とは?
定義(ここだけ押さえればOK)
自己相似(Self-Similarity/セルフ・シミラリティ)とは、
スケール(大きさ)を変えても、部分が全体と似た構造を保つ性質のことです。
ズームインしてもズームアウトしても“似た感じ”が続く——それが自己相似です。
2つのタイプ
完全自己相似:拡大・縮小してもまったく同じ形が現れるタイプ。
例)コッホ曲線(Koch curve)、シェルピンスキーの三角形(Sierpinski triangle)、カントール集合(Cantor set) などの数理フラクタル。
統計的自己相似:拡大・縮小でだいたい同じ(統計的に似ている)タイプ。
例)ロマネスコ、シダの葉、雲の輪郭、海岸線、山脈の稜線、川の分岐、都市の道路網。
フラクタル構造(Fractal structure)=自己相似が組み込まれた“形の仕組み”
フラクタル図形(Fractal figure)=フラクタル構造をもつ具体的な図形(上記の数理例など)
以下に関連語も整理します.
| 日本語 | 英語表現 | 補足説明 |
|---|---|---|
| フラクタル構造 | fractal structure | 自己相似性を持つ構造全般を指す。自然界・数学・デザインなどで使用。 |
| フラクタル図形 | fractal figure または fractal pattern | 具体的に描かれたフラクタル構造の図形(例:コッホ曲線など)。 |
| フラクタル幾何学 | fractal geometry | フラクタル構造を数学的に研究する分野。 |
| フラクタル次元 | fractal dimension | フラクタルの複雑さを数値で表す指標。 |
「フラクタル構造を持つ形」は英語で “a shape with a fractal structure”
「自然界のフラクタル構造」は “fractal structures in nature”
のように表現します。

やさしい数理の手触り(フラクタル次元)
フラクタルの“複雑さ”はフラクタル次元(Dimension/ディメンション)で表します。
直感だけ掴めば十分です。
たとえば、サイズをs倍に縮めると必要な“部品の数”がs^(-D)倍に増える——そんなべき乗則(Power law/パワー・ロウ)的な関係をもつ形が多いです。
具体的には、ボックスカウント法(小さな正方形で形を覆い、その個数N(ε)がスケールεに対してN(ε) ≈ ε^(-D)に従うかを見る)で見積もります。
海岸線の“長さが定まらない感じ”は、尺度を細かくするほど入り組みが増える=スケールで複雑さが再出現するからです。
覚え方:縮尺を変えても、似た複雑さが“また顔を出す”。
代表例(自然/数理/人工)
自然:ロマネスコ、シダ、雪の結晶、雲、山脈、川の分岐(ホートンの法則に沿う階層性)、海岸線のギザギザ など
数理:コッホ曲線、シェルピンスキー三角形、カントール集合、マンデルブロ集合(Mandelbrot set)(部分的・局所的に自己相似的な領域が見える)
人工・現象:都市形態(街区の階層性)、ネットワーク、テクスチャ生成、価格変動の“ざわつき”(スケールを変えても似た統計的ゆらぎを示すことがある)
「フラクタル構造」と「フラクタル図形」の関係
構造が抽象的な“性質”や“仕組み”を指し、
図形はそれを可視化した具体物(図・形)です。
数学で厳密に定義された図形(コッホ、シェルピンスキー、カントール等)は、完全自己相似の“教科書”。自然界はノイズや制約があるぶん、統計的自己相似として現れます。
無限鏡・ドロステ効果とのちがい(混同しないコツ)
無限鏡(インフィニティ・ミラー):
光が反射をくり返す物理現象で、奥行きが等間隔に並ぶ“連鎖”。
→ 形の縮尺が変わって似るわけではありません(自己相似ではない)。
ドロステ効果(Droste effect):
絵や写真の構図の中に“自分を含む自分”を入れ子で描く表現手法。
→ スケール全体で形の法則が保たれるとは限らず、作画の再帰が主題。
自己相似:
スケールをまたいで形の性質が保たれる(数理・自然のパターン)。
→ ロマネスコを割っても形の法則が続くのが好例。
ひとことで:
無限鏡=反射の連鎖(物理)/ドロステ=構図の再帰(表現)/自己相似=形の性質(数理・自然)。
なぜ注目されるのか?
心をつかむ理由(脳のはたらき)
スケールを超える一貫性:
拡大・縮小しても“同じらしさ”が続くと、脳は規則を素早く検出して安心します(処理のしやすさ=フルーエンシー)。
自然画像の“らしさ”:
自然界の景色はしばしば1/f型の空間周波数スペクトル(高周波と低周波のバランス)を持ち、多スケールの規則は見慣れた心地よさを生みます。
予測と驚きの両立:
“似ているが少しずつ違う”統計的自己相似は、予測できる安心と微差の驚きが同居。飽きずに見続けられる理由です。
使える理由(説明力と応用力)
複雑さを一言で要約できる:
フラクタル次元やべき乗則は、自然・社会の入り組みを短い指標で説明できます(海岸線、街の広がり、ネットワークの階層性など)。
マルチスケール設計に強い:
ロゴ・模様・UIの多段階グリッドや、建築・景観の階層的パターンづくりに有効。近くで見ても/遠くで見ても崩れない統一感を生みます。
CG/画像・音の生成:
手続き型(プロシージャル)テクスチャ、雲や山のノイズ合成、自然物のモデリングに自己相似の発想が活躍。
学びの入口:
数式が苦手でも、見れば腑に落ちる現象なので、理科・数学の導入教材として優秀。
いつの間にか“使っている”身近な場面
デザイン:同じモチーフを大・中・小のスケールで繰り返して一体感を出す(パッケージ、紙面レイアウト、パターン柄)。
園芸・造園:盆栽や植栽で、枝ぶりの階層を整えると“自然らしい”美しさが出る。
写真・映像:遠景→中景→前景に同じリズムの繰り返しを置くと、奥行きと統一感が増す。
学習・思考整理:章→節→項の入れ子構造は、情報をスケールで整理する“思考の自己相似”。
ここまでの要点(ひと息まとめ)
自己相似は、スケールをまたいで形の法則が続く性質。
フラクタル次元は、その複雑さの度合いを測る考え方。
無限鏡/ドロステとは原理も狙いも別。
私たちが心地よく感じるのは、規則と微差が共存する“自己相似のリズム”に、脳がよく馴染んでいるからです。
実生活への応用例
今日から使える“スケールの目”
学習:見て・撮って・言葉にするミニワーク
ねらい:「自己相似(Self-Similarity)」の“続く感じ”を体で理解する。
手順
素材を用意: ロマネスコ/シダの葉/松ぼっくり/多肉植物。
三段ズーム撮影: ①全体 → ②中くらい → ③部分の接写。
気づきを言語化: 「どこが似ている?どこが違う?」を短文で記録。
スケッチ: 大・中・小を1枚に重ね、繰り返しの“リズム”を線でなぞる。
ポイント: 3段階以上の縮尺をそろえると“続く感”が立ち上がります。
メリット: 抽象語(自己相似・縮尺・フラクタル)に手触りが出る。
デメリット: 自然物は完全一致でないため「違い」も必ず混ざる(=正常)。
仕事/デザイン:統一感と奥行きを同時につくる
狙い: 近くでも遠くでも破綻しない“多段階の一貫性”。
具体例
プレゼン資料: 見出し・小見出し・注釈で同じレイアウト原理(余白比・角丸・アイコン形)を 大・中・小で繰り返す → パッと見で筋が通る。
ロゴ/パターン: メインモチーフの簡略版(枝・葉・ドット等)を縮小して背景に疎密を変えながら配置 → うるさくない一体感。
UI設計: コンポーネントを階層化(カード→セル→チップ)し、角R・影・間隔をスケールに応じて相似的に調整 → 使い心地が安定。
※UI設計とは、「ユーザーインターフェース設計(User Interface Design)」の略で、人がアプリ・ウェブサイト・機械などを使いやすく操作できるように見た目や配置を設計することを指します。
メリット: 可読性、再利用性、ブランドの一貫性。
デメリット: やり過ぎると単調/“テンプレ感”。意図的な破調(1カ所だけ崩す)で回避。
写真・映像:スケールで物語る
演出レシピ
対置(たいち)ショット: ドローン遠景で分岐する川/道路網 → 直後に地上接写で枝葉/ひび割れ。似た分岐のリズムを続けて見せると、観客は「同じ法則が世界に貫かれている」感覚を得る。
三幕構成: 前景(大モチーフ)→ 中景(繰り返し)→ 遠景(群化)。同じ形質をスケールでつなぐと奥行きが濃くなる。
メリット: “わかった感”と“広がり”が同居する。
デメリット: 似すぎる画を連打すると飽和する。視点・光・比率を変化させる。
思考整理:自己相似なWBS(作業分解)
やり方: 目標→大課題→中課題→小タスクを似た文型で書く(動詞で始める・尺度ごとに所要時間帯を固定)。
効き目: 全体と部分の見通しが一致し、上から俯瞰/下から積上げが滑らかに噛み合う。
落とし穴: 細分化しすぎると管理コストが爆増。“3±1段”を目安に。
注意点・誤解されがちな点
よくある誤解
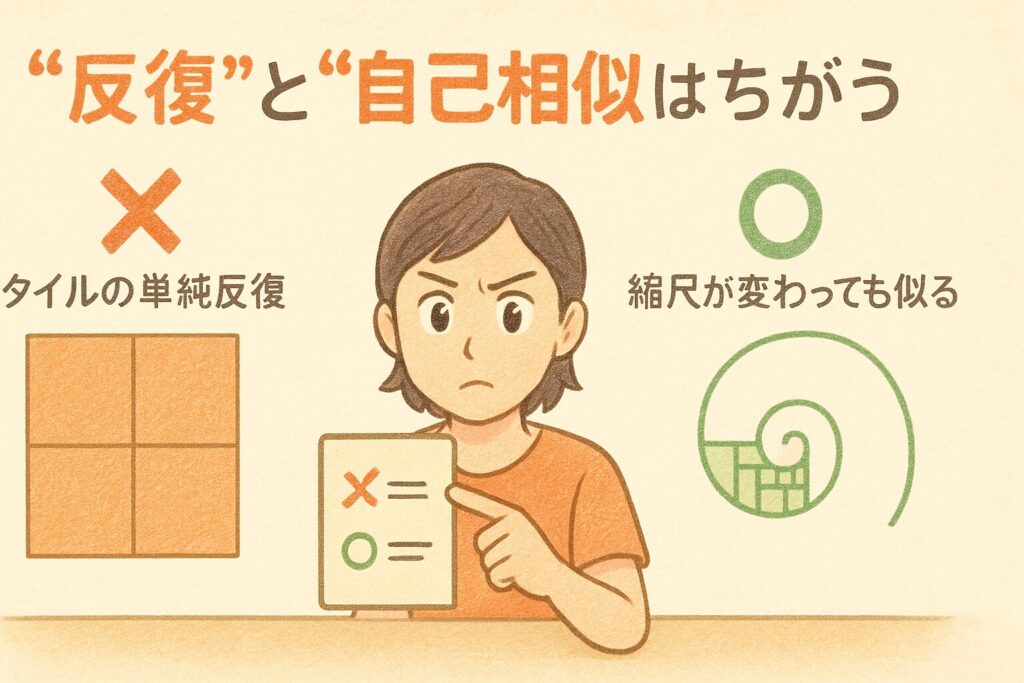
誤解①:「繰り返し模様=フラクタル」
→ 違います。 ただの反復(タイリング/周期パターン)はスケールが変わると規則が途切れます。自己相似は縮尺をまたいで似ることが条件。
誤解②:「自然は完璧な自己相似」
→ 違います。 自然は統計的自己相似(statistical self-similarity)。一定のスケール範囲で“だいたい似ている”傾向があるだけ。範囲外では崩れます。
誤解③:「無限鏡/ドロステと同じメカニズム」
→ 違います。 無限鏡=反射の連鎖(物理)、ドロステ=構図の再帰(表現)、自己相似=形の性質(数理・自然)。
誤解④:「グラフが斜めならパワー則」
→ 要注意。 両対数(log–log)直線は目測で錯覚しやすい。統計検定や対立仮説(対数正規など)との比較が必要。
※「パワー則」は「べき乗則(冪乗則、Power Law)」のことで、少数の要素が極めて大きな影響力を持つような、不均衡な法則を指します。
危険な考え方(NG)と理由
なんでもフラクタル化: 見立てが暴走すると説明が空疎に。→ 根拠のスケール範囲を必ず示す。
完全一致を強要: 自然は揺らぐ。→ “似て非なる”差分が魅力と理解。
装飾のための装飾: デザインで自己相似を足しすぎる。→ 主役の可読性が低下。
誤解が生まれるワケ(認知のクセ)
パターン過剰検出(アポフェニア): 人の脳は“意味のある繰り返し”を見つけすぎる傾向。
ズーム時代の見え方: スマホ拡大で“似て見える瞬間”だけ切り取ってしまう。
言葉の混同: 「反復」「相似」「再帰」「スケール不変(scale invariance)」の区別が曖昧。
回避ポイント(チェックリスト)
スケールを変える → 似ているか(最低3段階で確認)
どの範囲まで?(自己相似が成り立つスケール域をメモ)
目的は何?(説明/演出/学習…主役を決め、自己相似は引き立て役に)
対照を置く: 無限鏡=反射、ドロステ=構図、と横に並べて説明すると誤解が激減。
数字で補助: 余裕があればボックスカウントでフラクタル次元(fractal dimension)を概算し、“思い込み”を減らす。
ひと息まとめ
自己相似=縮尺をまたいで続く“形のリズム”。
使いどころ: 学習/デザイン/映像/思考整理の“統一感と奥行き”。
落とし穴: なんでもフラクタル視・完全一致幻想・対立仮説を見ない統計読解。
対策: 最低3スケール検証+範囲明記+目的の明確化。
おまけコラム
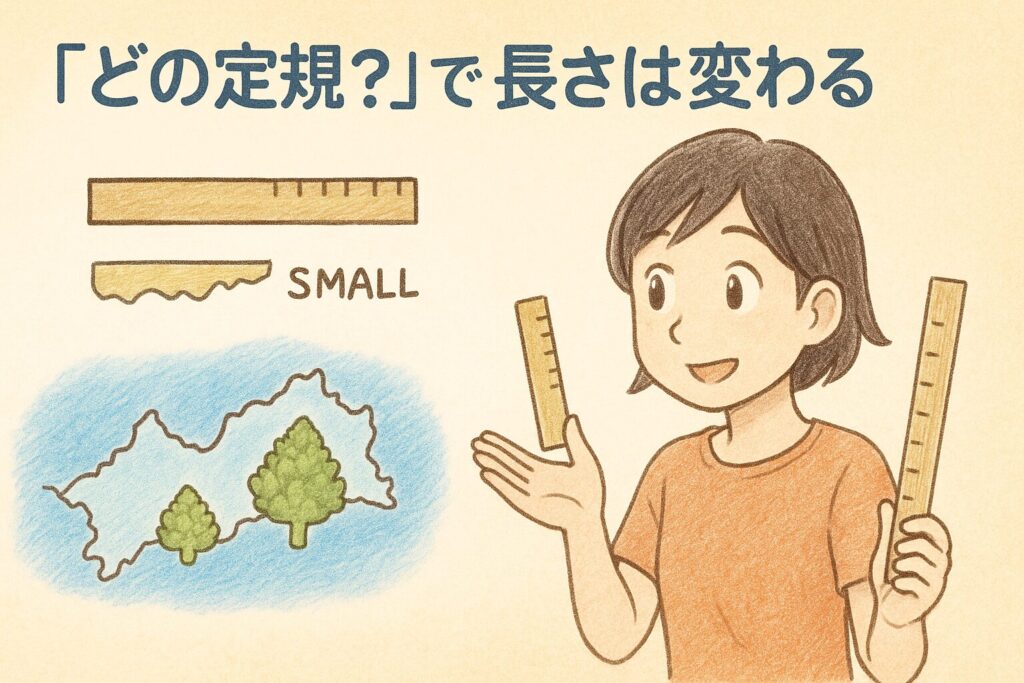
海岸線は“どの定規で測りますか?”
「海岸線の長さは定まらない(coastline paradox)」という有名な話題があります。発端は、フラクタル研究で知られるベノワ・マンデルブロ(Benoit Mandelbrot/マンドゥルブロ)による着想です。要点はとてもシンプルです。
短い定規を使うほど、海岸線の細かな凸凹をより多く拾う
→ 結果として“長さ”はどんどん伸びてしまう。
これは スケール依存(scale dependence/スケールに依存した測定値の変化) の直感的な例です。自己相似的なギザギザは、見る尺度で現れ方が変わります。
3つの身近な“定規”の変わり方
紙の地図と縮尺
1:2,500 の地図で湾の奥までなぞると長くなり、1:200,000 の地図では滑らかな線で短くなります。
アプリのズーム
地図アプリでズームインすると、岬や入り江の“細かい出入り”が増えて、計測線は伸びます。
ビジネスKPIの集計粒度
日次と5分粒度では“凸凹の見え方”が変わり、総移動量や変動量の評価がズレることがあります。――「どの定規で見るか」を決めない議論は、海岸線を“指で測る”のと同じです。
ナプキン実験(ボックスカウント風)
海岸線の写真に小さな正方形を重ね、正方形の一辺(ε)を半分に変えていきます。
必要なマスの数 N(ε) が、だいたい N(ε) ≈ ε^(-D) の関係を示せば、ここでいう D(ディー)=フラクタル次元(fractal dimension) の“雰囲気”を感じ取れます。
数式は覚えなくても大丈夫です。感覚としては、細かい定規ほど“複雑さがまた現れる”と捉えればOKです。
📌 教訓:測り方(スケール)を明示するだけで、議論の解像度が一段上がります。
・地図なら縮尺、データなら粒度、画像ならピクセルサイズを必ず添える。
・“長さ”“変動”“頻度”の議論は、定規の設定が肝心です。
まとめ・考察
スケールを渡る“似の言語”を手に入れる
3行で総括
自己相似(Self-Similarity)は、スケールが変わっても“似が続く”性質です。
自然では統計的自己相似として現れ、フラクタル次元という“複雑さの指標”で手触りよく捉えられます。
無限鏡=反射の連鎖(物理)/ドロステ=構図の再帰(表現)とは原理が異なり、自己相似=形の性質(数理・自然)です。
なぜ惹かれるのか(認知の視点)
私たちの脳は、多スケール(multi-scale)に通底する規則を見つけると「分かった!」という安心(処理のしやすさ)を得ます。同時に、“似て非なる”微差が驚きを保ち、飽きずに眺めてしまいます。予測と新鮮さが同居するリズム――それが自己相似の快さです。
今日から使える“自己相似の目”
学び:ロマネスコやシダを 全体→中→部分 の3段で観察・撮影し、似と違いを一言で言語化。
デザイン/UI:大・中・小で同じ設計原理(余白比・角R・影)を繰り返し、近景でも遠景でも破綻しない一貫性を。
説明と分析:グラフやKPIは粒度(定規)を明示。必要ならボックスカウントの概算で思い込みを減らす。
よくある落とし穴と橋のかけ方
なんでもフラクタル化しない:“このスケール範囲で” と領域を示す。
完全一致幻想を手放す:自然は統計的自己相似。“だいたいの似”こそが生命感。
類例混同を避ける:無限鏡(反射)/ドロステ(構図)との横並び比較を添えるだけで誤解は激減します。
考察
高尚な視点
自己相似は、複雑の中から秩序をすくい上げる“審美の道具”です。ズームの荒波に規則の糸を通すと、世界は断片から総体へと結び直されます。
ユニークな視点
思考も自己相似にできます。全体の主張→章→節→項を同じ文型(動詞始まり・一文要約)で“相似”に落とすと、読まれる文に変わります。
小さな宿題(週末15分)
被写体を1つ(ロマネスコ/シダ/雲/樹形)選ぶ
全体→中→部分の3枚を撮る
「同じなのはどこ?違うのはどこ?」を各15字で書く
余裕があれば、正方形グリッドでマスの数を比べてみる(感覚でOK)
最初の一歩は、定規を持ち替えること。
スケールが変わるたび、世界は同じ顔で、少し違う表情を見せます。
余韻のひと言
拡大の先にも縮小の先にも、“似の道筋”が続いていました。
その道を辿る目は、あなたの手の中にあります。
次のズームは、あなたの視点で。
――この先は、興味に合わせて“応用編”へ。
ここまでで「自己相似(Self-Similarity)」の基礎的な理解は十分です。
けれど、形の法則はここで終わりではありません。
スケールを変える視点を、言葉・思考・表現にも広げてみましょう。
つまり——「自己相似を“見る”」から、「自己相似を語る・使う」へ。
応用編
語彙を増やし、“自己相似”を語れる自分になる
① 言葉のフラクタルを探す
自己相似は形だけでなく、言葉の世界にも潜んでいます。
たとえば文章構成。
「序→破→急」や「起承転結」は、全体と各段落が似たリズムで構成される小さな自己相似です。
このように、文・段落・章が同じパターンで展開すると、読みやすく心地よいリズムが生まれます。
言葉の中にも“縮尺の似姿”があると気づくと、書く力・話す力が変わります。
② 日常の“自己相似”を語る練習
身近なものを1つ選ぶ(木の枝、道路の分岐、音楽のリズム、料理の盛り付け)
「全体→部分→細部」を観察して、似ている箇所を3つ書く
「〇〇も××も、どちらも△△の形をしている」と一文でまとめてみる
これを繰り返すと、自分の観察と言葉に“スケール感”が宿るようになります。
たとえば:
「街の道路網も、私の一日の動きも、“中心から枝分かれする”リズムをもっている。」
こうした気づきの積み重ねが、「自己相似を語れる言葉」を増やしてくれます。
③ 思考を“自己相似”に整理する
発想や企画を立てるときも、大きなアイデアを小さく分けても“似た構造”を保つと、筋の通った構成になります。
たとえば:全体テーマ → サブテーマ → 具体例
会社の理念 → 部署目標 → 個人タスク
どのスケールでも同じリズムでつながっていると、迷わず行き来できるのです。
これはまさに「思考のフラクタル設計」。
💬 次への橋渡し
ここまで来たあなたは、もう“形を観る人”ではなく、
“形を語り、使う人”の入り口に立っています。
日常の中で「似ている」と感じた瞬間を、
ぜひあなたの言葉で書きとめてください。
それは、世界の複雑さをやさしく解く最初の一文になるでしょう。
💡この先の学び方ヒント
語彙を増やす:自己相似・フラクタル・スケール不変(scale invariance)・パワー則(power law)
観察を続ける:拡大/縮小の両方から見る癖をつける
表現を磨く:似のリズムを文やデザインで再現してみる
更に学びたい人へ
📚 書籍紹介
初学者・小学生にもおすすめ
『フラクタル : 混沌と秩序のあいだに生まれる美しい図形』
著者: オリヴァー・リントン(翻訳:駒田 曜)
特徴:コンパクトながら多くのフラクタル図形(ジュリア集合・コッホ曲線など)を美しい図版とともに紹介。自然界と数理の橋を視覚的に感じられる入門書。
おすすめ理由:拡大しても同じ形が現れる“フラクタル図形”の直感を掴むのに最適。図や写真が豊富なため、小学生~初学者でも安心して読めます。
中級者向け(数理の手触りを知りたい人へ)
『フラクタルって何だろう : 新しい科学が自然を見る目を変えた』
著者: 高安 秀樹・高安 美佐子
特徴:自然界(山、雲、株価変動など)に現れるフラクタルの実例を多数取り上げ、読み物としても楽しめる構成。
おすすめ理由:数理的な背景を少しずつ理解したい人向け。自己相似・フラクタル構造を「なぜ?」という視点で掘り下げられます。
全体におすすめ(もう一歩深く)
『フラクタル科学 (新装版)』
著者:高安 秀樹(編著)
特徴:自然科学・複雑系・スケール不変・統計的自己相似など、フラクタル現象の“理論的・応用的な視点”を幅広く解説。
おすすめ理由:中級〜上級者向け。形の法則をデザイン・分析・研究に活かしたい人、数理的背景を深めたい人に特に有益です。
🗺 縁の地・体験できる場所
中谷宇吉郎 雪の科学館(石川県加賀市)
雪の結晶という“自己相似を伴う自然現象”をテーマにした科学館。観察・展示体験を通じて、形の“繰り返し・縮尺感”を直接感じられる場です。
おすすめポイント:理論だけでなく「実物・見えるもの」で学びを深めたい人に適しています。
名古屋市科学館(愛知県名古屋市)
光・鏡・視覚に関する展示が充実しており、スケール感・反射・構図といった“見え方の法則”を体感できる環境。
おすすめポイント:家族連れ・初めて科学館に行く人にも入りやすく、日常に戻ってから“自分の観察眼”を育てる場としても人気です.
日本科学未来館(東京都お台場)
自然・計算・生成の交差点として、マルチスケール・複雑系・形の生成に関する展示がある施設。
おすすめポイント:自己相似の“数理/生成”側に興味がある人、将来的に創作・研究にも使える知見を得たい人に向いています。
読書+体験の両輪で“自己相似”という視点を、言葉と感覚の両面から深めていきましょう。
🌿 疑問が解決した物語
翌朝。
美咲は、昨日のロマネスコの小さなツブを思い出しながら、理科ノートを開きました。
学校で先生に「これってどうして同じ形が続くんですか?」と聞いてみると、
先生は黒板に螺旋(らせん)を描きながら言いました。
「それはね、“自己相似(セルフ・シミラリティ)”っていう自然の法則なんだよ。
大きくしても小さくしても、同じ形が現れる。
つまり、“部分が全体に似る”という、自然がもつ秩序なんだ。」
その言葉に、美咲の目が少し輝きました。
家に帰ると、スマホで雪の結晶やシダの葉を調べ、
「これも自己相似だ!」と声を上げました。
形がつながっている――世界の中に、同じリズムが響いている。
それがわかった瞬間、昨日までの「なんで?」が
静かに「そういうことだったんだ」に変わっていきました。
美咲はノートの片隅に、こう書きました。
“似ているって、つながっているってことなんだ。”
それからというもの、彼女はものを見る目が少し変わりました。
木の枝も、雲の形も、水の流れも——
どれもが“全体の中の一部”として、同じリズムを繰り返しているように見えたのです。
そして、そっとつぶやきました。
「自然って、まるで大きな絵の一部分みたいだね。」

🌱 教訓と問いかけ
学び:
自己相似は「似ている」を超えた、“世界のつながりの形”。
その法則を知ることで、身の回りのあらゆるものが
少しだけ違って、少しだけ同じ——そんな“生命のリズム”でできていると気づけます。
行動:
美咲のように、まずは身近な“形の繰り返し”を見つけてみましょう。
野菜の断面、木の枝、雲の写真。
見つけたら、それを描く・撮る・比べる。
観察が、理解の第一歩になります。
読者への問いかけ:
あなたのまわりには、どんな“似ている形”がありますか?
一度、立ち止まって見てください。
きっとそこにも、小さな自己相似の世界が広がっています。
🌸 文章の締めとして
ふとした瞬間に目にする“似ている形”——それは、
自然や数式の中だけでなく、私たちの毎日の中にも quietly(そっと)息づいています。
ロマネスコのツブを見つめた美咲のように、
何かの「くり返し」にハッとした経験、あなたにもあるかもしれません。
それは、退屈な日常の中にひそむ「リズム」への気づき。
小さな違いの中に、同じ調べが流れていることを感じたとき、
世界は少しやさしく、そして深く見えてきます。
“自己相似”という言葉は、難しい理屈ではなく、
「どんなスケールでも、同じ思いが通っている」という
自然と私たちの共通の“まなざし”を教えてくれます。
だからこそ、次に何かを見つめるとき、
「どこかで見たような形だな」と感じたら——
それをただの“偶然”で片づけずに、
“世界の中のリズム”として感じ取ってみてください。
🪞補足注意
本記事の内容は、著者自身が信頼できる基礎知識と公開された資料をもとに、
著者が自分で確かめられる範囲を大切にまとめたものです。
ここで語った“自己相似(セルフ・シミラリティ)”は、あくまで自然の中の一側面。
見る角度、測るスケール、時代の研究によって、解釈は少しずつ変わっていくものです。
つまり、これは「唯一の正解」ではなく、
あなた自身の観察と思索が続いていくための“はじまりのかたち”です。
自然の形には例外があり、曖昧さがあり、そしてそれこそが面白さ。
同じ“似ている”という現象の中にも、無数の物語が潜んでいます。
だからこそ、この記事をきっかけに、ぜひあなたの視点で“似の世界”を見つけてください。
図鑑でも、科学書でも、展覧会でも構いません。
あなたの目に映る“もうひとつの自己相似”を探してみましょう。
観察を重ねるほどに、形の奥にあるリズムが、
まるで静かに呼吸しているように感じられるはずです。
そしてそのとき、きっと気づくでしょう——
知ることも、学ぶことも、繰り返しながら深まっていく。
それもまた、この世界の 自己相似 なのです。

最後まで読んでいただき、
本当にありがとうございました。
それは、自然の法則でもあり、
生きることの姿そのものでもあるのです。
そして、あなたの中にも、きっと続いているはずです。
——見つめるたびに新しく、でもどこか同じ。
それが、この世界の 自己相似(セルフ・シミラリティ)。







コメント